Statistik
Leon
Civilingenjör i farkostteknik - KTH
0 min. läsning
för 2 år sedan



Både medelvärdet och medianen har sina användningsområden beroende på sammanhanget och målen med din analys. Att förstå skillnaderna mellan dem är viktigt för att kunna använda rätt mått för rätt situation.
Videogenomgång av området Statistik
Medelvärde
Medelvärdet är en av de mest grundläggande måtten inom statistiken och representerar "genomsnittet" av en datamängd. För att beräkna medelvärdet, adderar du alla värden i datamängden och delar summan med antalet observationer.
Medelvärdet är användbart när du vill ha en generell uppfattning om datamängden och när du vill få en känsla av "genomsnittet" av värdena. Det är dock viktigt att vara medveten om att medelvärdet kan påverkas av extremvärden (outliers) och inte alltid återspegla "typvärdet" i datan.
Låt oss ta ett exempel för att förklara detta i detalj. Antag att vi har en datamängd som består av fem betyg: 80, 85, 90, 95 och 100.
För att beräkna medelvärdet, adderar vi alla betyg och dividerar med antalet observationer (i det här fallet 5):
$\text{Medelvärde} = \frac{80 + 85 + 90 + 95 + 100}{5} = \frac{450}{5} = 90$
Så medelvärdet för betygen är 90.
Median
Medianen är det mittvärde i en datamängd som delar datan i två lika delar när den är sorterad i stigande ordning. Det innebär att hälften av observationerna är större än medianen, och hälften är mindre än medianen.
Låt oss använda samma datamängd som tidigare för att beräkna medianen:
Först sorterar vi datan i stigande ordning: 80, 85, 90, 95, 100.
Eftersom vi har en udda mängd observationer (5 i det här fallet), är medianen det mittvärde, vilket i det här fallet är 90. Om det är ett jämnt antal tal så tar man medelvärdet av de två talen i mitten istället.
För att förstå medianens fördelar, tänk på situationer där du har datamängder med extremvärden eller outliers. Medelvärdet kan dras uppåt eller nedåt av dessa extremvärden och ge en missvisande uppfattning om "genomsnittet" av de vanliga värdena. Medianen är mindre känslig för extremvärden och ger en bättre uppfattning om det typiska värdet i datamängden.
Både medelvärdet och medianen har sina användningsområden beroende på sammanhanget och målen med din analys. Att förstå skillnaderna mellan dem är viktigt för att kunna använda rätt mått för rätt situation.
Erik frågade sina 29 klasskamrater hur många timmar de hade pluggat under föregående helg. Svaren redovisas i ett stolpdiagram.
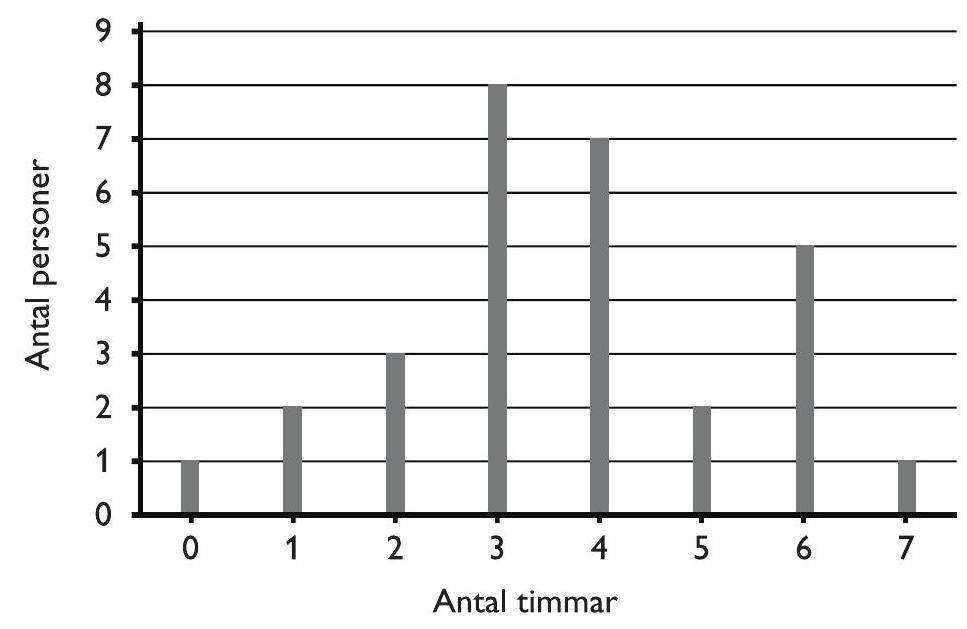
Vad är medianen för svaren som Erik fick?
Öva på Statistik
Öva på Statistik genom att lösa uppgifter som kommer på högskoleprovet.
Relaterade artiklar
Sannolikhet
Sannolikhet handlar om att mäta hur troligt det är att en händelse kommer att inträffa. Det hjälper oss att förstå och kvantifiera osäkerhet och risk inom olika situationer. Sannolikhet är en central del av statistik och används i många aspekter av vårt dagliga liv. Sannolikhet är användbart inom många områden, inklusive spelteori, statistik, och riskanalys. Det hjälper oss att fatta beslut och förutse resultat i en mängd olika situationer. Enkelt sannolikhetsuppgifter dyker frekvent upp på högskoleprovet så detta är något du måste förstå för att prestera bra på kvantitativa delen.

Mathilde
3 min. läsning
2024-03-16
Procent
Detta är en grundläggande översikt av procent i matematiken. Procent används i många olika sammanhang, inklusive ekonomi, handel, och procentuell ökning och minskning. Det är ett användbart koncept för att förstå hur en del förhåller sig till en helhet.

Mathilde
1 min. läsning
2024-03-16
Funktioner
En funktion i matematiken är som en maskin som tar ett nummer som inmatning och ger oss ett annat nummer som utmatning. Du kan tänka på det som en regel som beskriver hur ett nummer förändras till ett annat. En funktion representeras oftast som $f(x)$ eller $y$, där $x$ är ingången (ingångsvärdet) och $f(x)$ eller $y$ är utgången (resultatet).

Morgan
0 min. läsning
2024-03-16