Geometri
Mathilde
UX Designer - Stockholms universitet
2 min. läsning
för ett år sedan
Geometri är en gren inom matematiken som handlar om att studera former, storlekar och egenskaper hos objekt i rummet. Dessa objekt kan vara allt från linjer och cirklar till tre-dimensionella former som kuber och koner.
Grundläggande Begrepp
1. Punkt: Den mest grundläggande enheten i geometri. Det är en position i rummet och har ingen storlek.
2. Linje: En rät linje består av en samling punkter som sträcker sig i båda riktningarna. Linjer kan vara oändligt långa.
3. Rät Vinkel: En vinkel som är 90 grader.
4. Triangel: En polygon med tre sidor. Det finns olika typer av trianglar, inklusive liksidiga (alla sidor och vinklar är lika) och rätvinkliga (en vinkel är 90 grader). Vinkelsumman av en triangel summerar till 180 grader
5. Kvadrat: En fyrkant där alla sidor är lika långa. Alla vinklar är 90 grader och vinkelsumman summerar till 360 grader.
6. Rektangel: En fyrkant där basen och höjden inte är lika långa. Alla vinklar är 90 grader och vinkelsumman summerar till 360 grader.
7. Cirkel: En uppsättning punkter som är lika avstånd från en central punkt, kallad centrum.
Triangel
En polygon med tre sidor. Det finns olika typer av trianglar, inklusive liksidiga (alla sidor och vinklar är lika) och rätvinkliga (en vinkel är 90 grader). Vinkelsumman av en triangel summerar till 180 grader.
För att beräkna omkretsen av en triangel summerar vi längden av triangelns tre sidor.
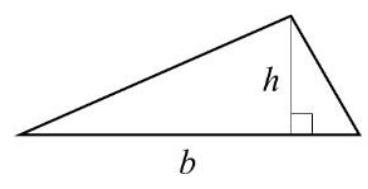
För att beräkna arean av en triangel används formeln:
$$A=\frac{b h}{2}$$
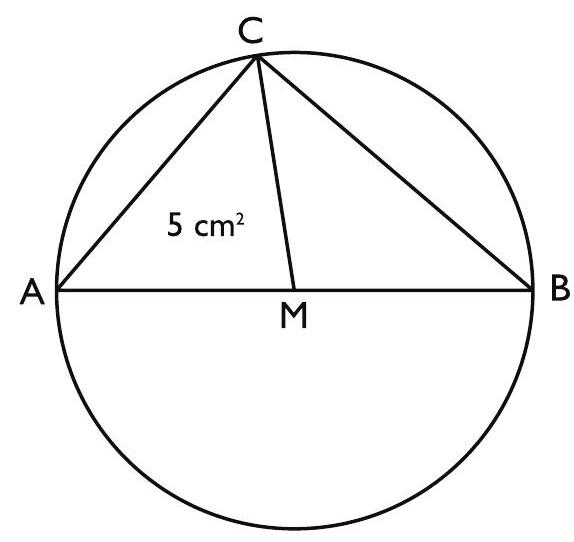
Triangeln $A B C$ är inskriven i en cirkel. Cirkelns medelpunkt $M$ ligger på sidan $A B$. Arean för triangeln $A C M$ är $5 \mathrm{~cm}^{2}$. Vilken area har triangeln $A B C$?
Cirkel
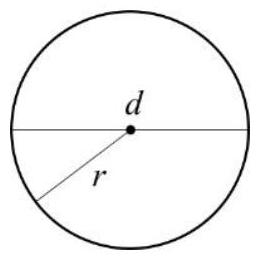
För att beräkna omkretsen av en cirkel använder vi formeln:
$$O=2 \pi r=\pi d$$
För att beräkna arean av en cirkel används formeln:
$$A=\pi r^{2}=\frac{\pi d^{2}}{4}$$
En cirkels omkrets är $2 \pi \mathrm{cm}$. Hur många grader är den cirkelsektor vars cirkelbåge har längden $\frac{2 \pi}{3} \mathrm{~cm}$?
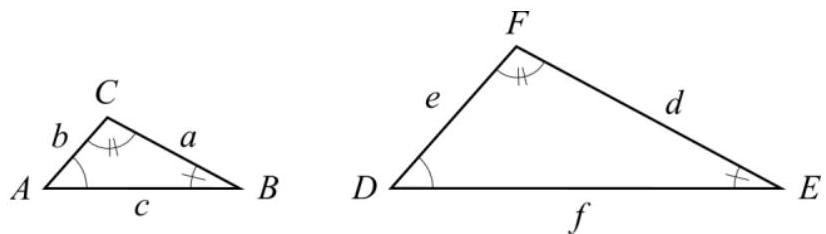
Trianglarna ABC och DEF är likformiga om:
$$\frac{a}{d}=\frac{b}{e}=\frac{c}{f}$$
$A B C$ är en triangel. $D E$ är parallell med $A C$, och $D E=B D$. Vad är $x$?
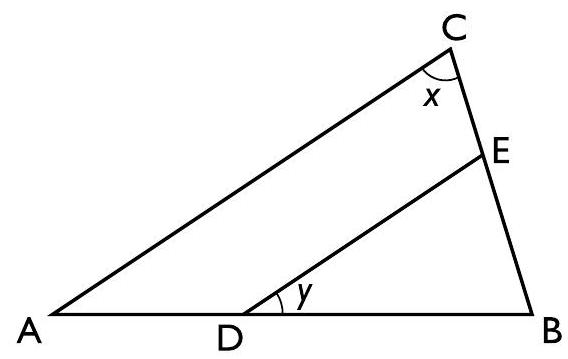
Topptriangelsatsen
$$\frac{D E}{A B}=\frac{C D}{A C}=\frac{C E}{B C}$$
Transversalsatsen:
$$\frac{C D}{A D}=\frac{C E}{B E}$$
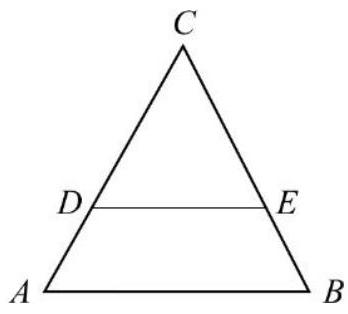
DE är parallell med AB
Bisektrissatsen
$$\frac{A D}{B D}=\frac{A C}{B C}$$
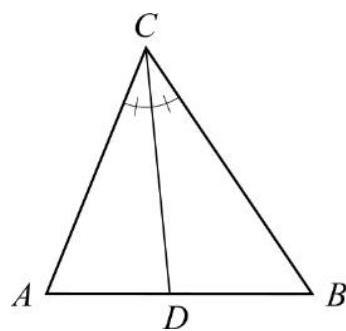
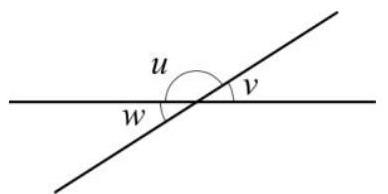
Vinklar
Sidovinklar: $ u+v=180^{\circ} $
Vertikalvinklar: $ w=v $
$L_{1}$ skär två parallella linjer $L_{2}$ och $L_{3}$
Likbelägna vinklar: $v=w $
Alternatvinklar: $u=w $
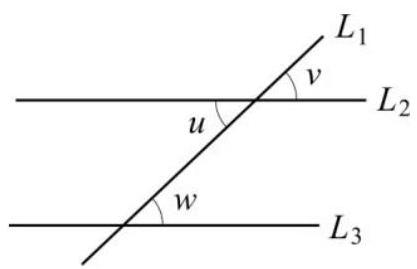
Linjerna $L_{1}$ och $L_{2}$ är parallella.
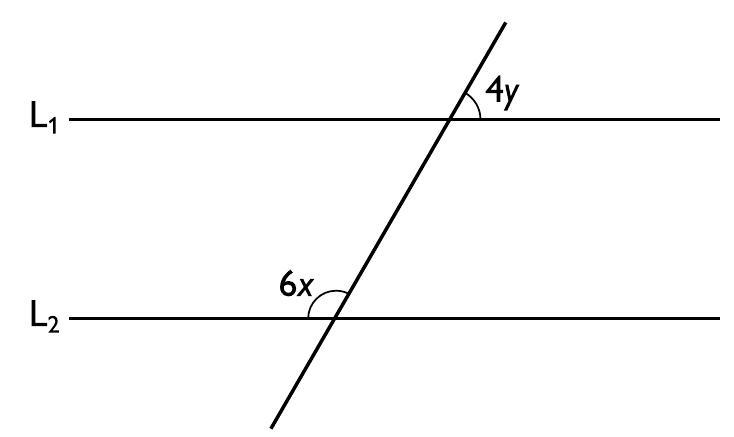
Vad är $3 x+2 y$?
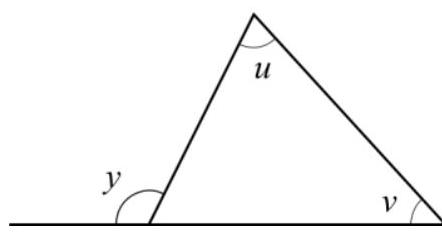
Yttervinkelsatsen
$$y=u+v$$
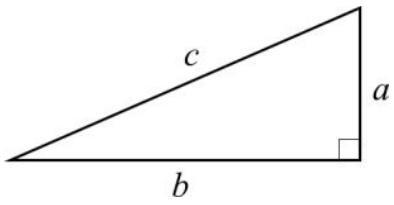
Pythagoras sats
Pythagoras sats är en grundläggande och klassisk matematisk relation som gäller för rätvinkliga trianglar. Det är namngivet efter den grekiska matematikern Pythagoras och säger att i en rätvinklig triangel, där en av vinklarna är 90 grader (rät vinkel), är summan av kvadraterna på de två kateterna (de två sidorna som möter den räta vinkeln) lika med kvadraten på hypotenusan (den längsta sidan, som är motsatt den räta vinkeln). Pythagoras sats dyker väldigt ofta upp på högskoleprovet och det rekommenderas att göra många uppgifter på detta områden för att garantera poäng under provet. Formeln för Pythagoras sats är:
$$ a^2 + b^2 = c^2 $$
Där:
- $a$ och $b$ representerar längderna på kateterna.
- $c$ representerar längden på hypotenusan.
Detta är ett kraftfullt verktyg inom geometri och används ofta för att lösa problem som innefattar rätvinkliga trianglar. Pythagoras sats är en grundläggande regel och har många praktiska tillämpningar inom olika områden av matematik och vetenskap, inklusive arkitektur, fysik och konstruktion.
Dessutom kan Pythagoras sats omformuleras på olika sätt för att hitta olika storheter. Här är några exempel på hur man kan omformulera satsen:
1. Att hitta hypotenusan (c):
$$c = \sqrt{a^2 + b^2}$$
Om du har längderna på båda kateterna kan du använda denna formel för att beräkna längden på hypotenusan.
2. Att hitta en katet (a eller b):
$$a = \sqrt{c^2 - b^2}$$ eller $$b = \sqrt{c^2 - a^2}$$
Om du har längden på hypotenusan och en av kateterna, kan du använda dessa formler för att beräkna den andra kateten.
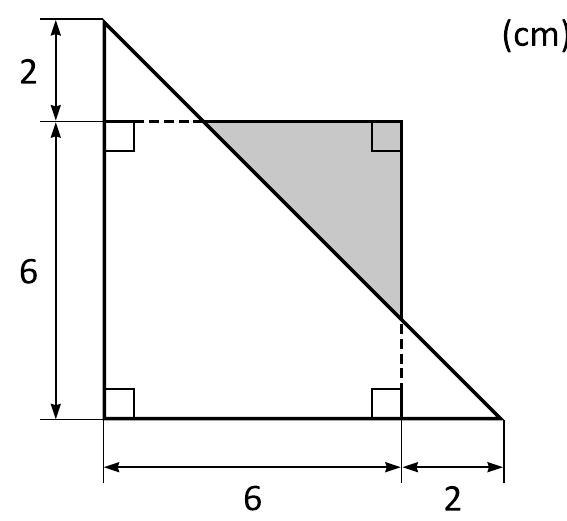
Kvantitet 1
Arean av den skuggade ytan
Kvantitet 2
$6 \mathrm{~cm}^{2}$
De vanligaste formlerna som används på högskoleprovet är följande:
Likbelägna vinklar:
$$v=w $$
Alternatvinklar:
$$u=w $$
Sidovinklar:
$$ u+v=180^{\circ} $$
Vertikalvinklar:
$$ w=v $$
Pythagoras sats:
$$ a^2 + b^2 = c^2 $$
Öva på Geometri
Öva på Geometri genom att lösa uppgifter som kommer på högskoleprovet.
Relaterade artiklar
Sannolikhet
Sannolikhet handlar om att mäta hur troligt det är att en händelse kommer att inträffa. Det hjälper oss att förstå och kvantifiera osäkerhet och risk inom olika situationer. Sannolikhet är en central del av statistik och används i många aspekter av vårt dagliga liv. Sannolikhet är användbart inom många områden, inklusive spelteori, statistik, och riskanalys. Det hjälper oss att fatta beslut och förutse resultat i en mängd olika situationer. Enkelt sannolikhetsuppgifter dyker frekvent upp på högskoleprovet så detta är något du måste förstå för att prestera bra på kvantitativa delen.
Mathilde
3 min. läsning
2024-03-16
Kvadratuttryck
Kvadratuttryck är användbara inom algebra för att förenkla ekvationer, lösa problem med andragradsekvationer och för att förstå polynomens egenskaper.
Morgan
0 min. läsning
2024-03-16
Funktioner
En funktion i matematiken är som en maskin som tar ett nummer som inmatning och ger oss ett annat nummer som utmatning. Du kan tänka på det som en regel som beskriver hur ett nummer förändras till ett annat. En funktion representeras oftast som $f(x)$ eller $y$, där $x$ är ingången (ingångsvärdet) och $f(x)$ eller $y$ är utgången (resultatet).
Morgan
0 min. läsning
2024-03-16