Vinkelräta linjer
Nora
Läkare - Karolinska Institutet
2 min. läsning
för ett år sedan
Vinkelräta linjer är en annan viktig relation mellan linjer i ett koordinatsystem och innebär att de möts vid en vinkel av exakt 90 grader. Denna egenskap finner stort värde i geometri och analys av linjära ekvationer.
Definition av vinkelräta linjer
Två linjer är vinkelräta mot varandra om de skär varandra med en vinkel på $90^\circ$. Denna relation har en specifik algebraisk egenskap baserat på linjernas lutning.
Algebraisk egenskap
Om två linjer är vinkelräta mot varandra, då är produkten av deras lutningar $k_1$ och $k_2$ lika med $-1$. Alltså:
$$ k_1 \cdot k_2 = -1 $$
Detta innebär att lutningen på den ena linjen är den negativa inversen av lutningen på den andra linjen.
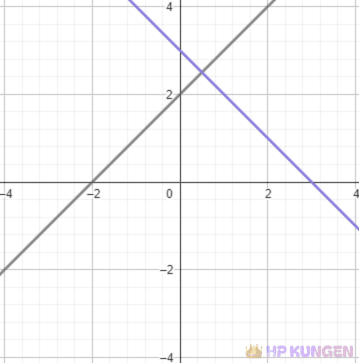
Vinkelräta linjer
Vinkelräta linjer: Matematisk formulering
Om vi har två linjer med ekvationerna:
Linje 1: $y = k_1x + m_1$
Linje 2: $y = k_2x + m_2$
Där $k_1$ och $k_2$ är lutningarna för respektive linje. Om linjerna är vinkelräta, då gäller:
$$ k_1 \cdot k_2 = -1 $$
Invers lutning
För att förstå detta, om en linje har en lutning $k$, kommer den vinkelräta linjen ha en lutning $\frac{-1}{k}$.
Vinkelräta linjer: Grafisk representation
När du ritar vinkelräta linjer i ett koordinatsystem:
Rita den första linjen: För en given lutning $k_1$ och $y$-intercept $m_1$, rita linjen.
Hitta den vinkelräta linjens lutning: Beräkna den vinkelräta lutningen som $k_2 = -1/k_1$.
Rita den andra linjen: Använd lutningen $k_2$ och rita linjen som passerar genom skärningspunkten för att visualisera $90^\circ$-vinkeln mellan dem.
Exempel
Låt oss säga att vi har en linje med ekvationen $y = 2x + 3$. För att hitta en vinkelrät linje, måste lutningen för den andra linjen vara $-1/2$ (eftersom $2 \times (-1/2) = -1$). Den vinkelräta linjen kan exempelvis ha en form som $y = -\frac{1}{2}x + c$, där $c$ är vilken konstant som helst beroende på var linjen skär $y$-axeln.
Relaterade artiklar
Medicinska termer
Medicinska termer, precis som många andra typer av teknisk terminologi, innehåller ofta prefix och suffix som används för att ändra eller förtydliga betydelsen av ett grundord (stam). Att lära sig dessa kan göra att du enkelt kan utesluta många svarsalternativ på ord-delen på högskoleprovet. Nedan finner du en lista på några vanliga suffix och prefix som kan vara bra att kunna.
Nora
1 min. läsning
2024-03-16
Tekniska termer
Många delar av högskoleprovet inkluderar tekniska och naturvetenskapliga frågor där användningen av specialiserad terminologi är oundviklig. Behärskningen av dessa termer är inte bara central för att korrekt tolka och svara på tekniska frågor, utan underlättar också förståelsen av komplexa tekniska texter. Nedan är en lista på prefix och suffix som är bra att känna till för att maximera dina chanser att skriva högt på högskoleprovet.

Leon
1 min. läsning
2024-03-16
XYZ-delen
XYZ handlar om matematisk problemlösning och är en av de mest grundläggande färdigheterna inom matematik. Det handlar inte bara om att räkna ut ekvationer eller memorera formler, utan om förmågan att tänka kreativt och logiskt för att lösa problem. Första delen på högskoleprovets kvantitativa del är 24 uppgifter matematisk problemlösning som har en uppskattad lösningstid på 24 minuter, eller 1 minut per uppgift.
Daniel
2 min. läsning
2024-03-14