Skärningspunkt mellan räta linjer
Daniel
Civilingenjör i datateknik - KTH
0 min. läsning
för ett år sedan
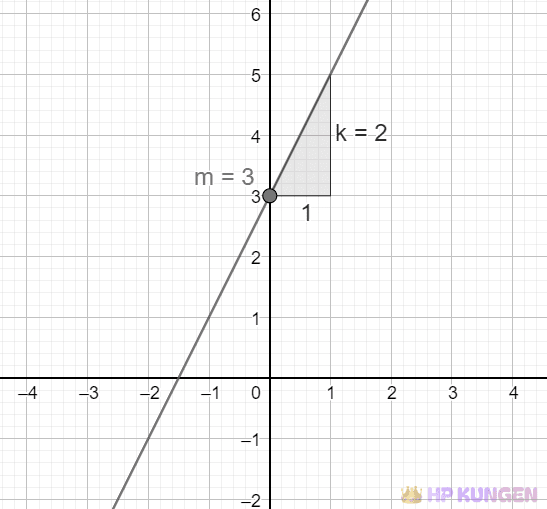



Skärningspunkten mellan två räta linjer är den punkt där linjerna korsar varandra. För att bestämma denna punkt måste vi hitta ett gemensamt $(x, y)$-värde som uppfyller båda linjernas ekvationer. Detta innebär att båda ekvationerna har samma $y$-värde för samma $x$-värde på detta gemensamma punkt.
Att finna skärningspunkten
Låt oss säga att vi har två räta linjer:
$y = k_1x + m_1$
$y = k_2x + m_2$
Målet är att hitta ett par $(x, y)$ som uppfyller båda dessa ekvationer samtidigt.
Eftersom båda uttrycken är lika med $y$, kan vi sätta linjernas ekvationer lika med varandra:
$$ k_1x + m_1 = k_2x + m_2 $$
Här är $k_1$ och $m_1$ lutningen och skärningen för den första linjen och $k_2$ och $m_2$ för den andra linjen. Vi löser denna ekvation för $x$ för att hitta x-värdet där linjerna skär varandra.
Lösa ekvationen för $x$
Först löser vi ekvationen:
$$ k_1x + m_1 = k_2x + m_2 $$
Börja med att samla alla termer innehållande $x$ på ena sidan och konstanter på den andra:
$$ k_1x - k_2x = m_2 - m_1 $$
Faktorisera ut $x$:
$$ x(k_1 - k_2) = m_2 - m_1 $$
Nu kan vi lösa för $x$ genom att dividera båda sidor med $(k_1 - k_2)$, antar att de inte är lika (om $k_1 = k_2$ är linjerna parallella och har ingen skärningspunkt):
$$ x = \frac{m_2 - m_1}{k_1 - k_2} $$
Hitta $y$-värdet
När vi nu har ett $x$-värde, sätter vi in det i någon av ursprungliga linjens ekvationer för att finna $y$-värdet. Det spelar ingen roll vilken ekvation du använder, så länge uttrycken är korrekta, eftersom de båda borde ge samma $y$-värde vid $x$-koordinaten för skärningspunkten:
$$ y = k_1 \left(\frac{m_2 - m_1}{k_1 - k_2}\right) + m_1 $$
eller
$$ y = k_2 \left(\frac{m_2 - m_1}{k_1 - k_2}\right) + m_2 $$
Sammanfattning
Så för att hitta skärningspunkten mellan två räta linjer:
Sätt linjernas ekvationer lika med varandra för att hitta $x$.
Lösa ekvationen för $x$.
Sätt in $x$-värdet i någon av linjernas ekvationer för att få $y$.
Det uppfunna $(x, y)$-paret är din skärningspunkt.
Det här är en metod som kommer till nytta vid högskoleprovet och även i matematik eftersom skärningspunkterna kan utnyttjas i olika tillämpningsproblem och geometri.
Relaterade artiklar
DTK-delen
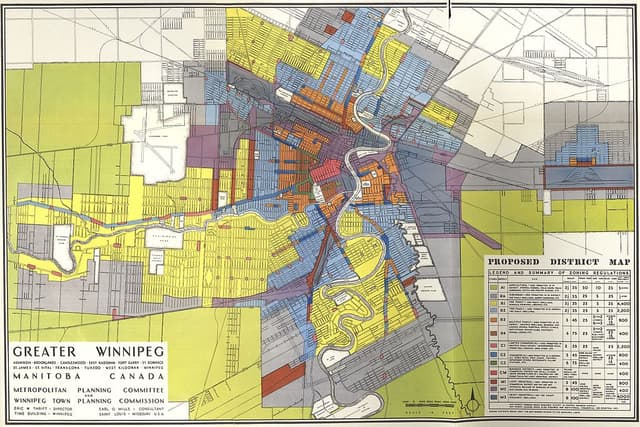
DTK-delen på högskoleprovet handlar om "Diagram, Tabeller och Kartor." Denna del testar din förmåga att tolka och använda information som presenteras i grafisk form, inklusive diagram, tabeller och kartor. Här är en grundläggande förklaring av denna del:
Leon
3 min. läsning
2024-03-30
Tekniska termer
Många delar av högskoleprovet inkluderar tekniska och naturvetenskapliga frågor där användningen av specialiserad terminologi är oundviklig. Behärskningen av dessa termer är inte bara central för att korrekt tolka och svara på tekniska frågor, utan underlättar också förståelsen av komplexa tekniska texter. Nedan är en lista på prefix och suffix som är bra att känna till för att maximera dina chanser att skriva högt på högskoleprovet.

Leon
1 min. läsning
2024-03-16
Ekonomiska termer
Högskoleprovet inkluderar ofta texter eller ord som relaterar till samhällsvetenskap och ekonomi, där användningen av specialiserad terminologi är oundviklig. Att behärska dessa termer är inte bara nyckeln till att korrekt tolka och svara på frågor utan underlättar även förståelsen texterna i LÄS-delen. Nedan är en lista på vanliga prefix och suffix som är bra att känna till inför ORD-delen på högskoleprovet.

Morgan
1 min. läsning
2024-03-16