Lodräta linjer
Nora
Läkare - Karolinska Institutet
2 min. läsning
för ett år sedan
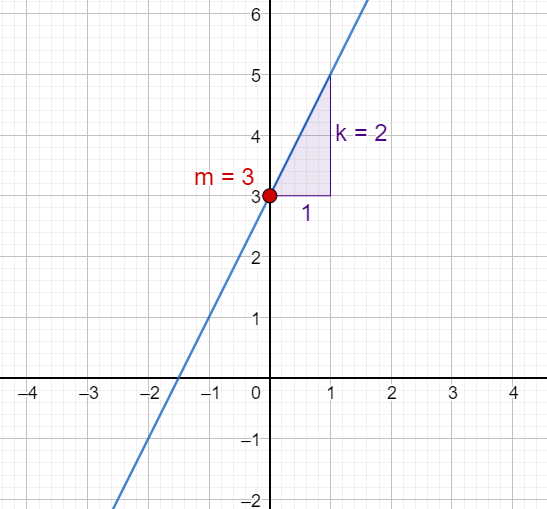



När vi talar om lodräta linjer i ett koordinatsystem, refererar vi till de speciella typer av linjer som har en konstant $x$-koordinat oavsett $y$-värdets variation. Dessa lodräta linjer skiljer sig från de flesta vanliga räta linjer, som vanligtvis uttrycks i formen $y = kx + m$.
Definition av lodräta linjer
En lodrät linje är en linje där alla punkter på linjen har samma $x$-koordinat. Detta innebär att oavsett vilket $y$-värde du väljer, kommer $x$-värdet alltid att vara konstant.
Ekvation för en lodrät linje
Ekvationen för en lodrät linje kan skrivas som:
$$ x = a $$
Här representerar $a$ den fasta $x$-koordinat där linjen ligger. Varje punkt på denna linje kan skrivas som $(a, y)$, där $y$ kan vara vilket värde som helst, positivt, negativt eller noll.
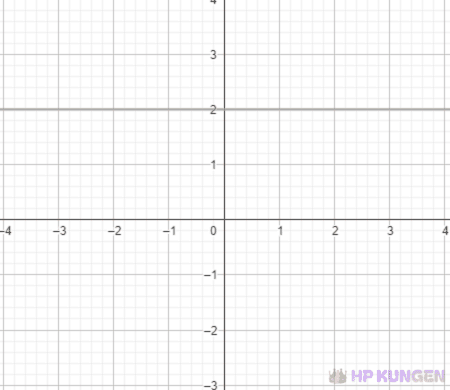
Lodrät linje: y = 2
Egenskaper hos lodräta linjer
Ingen lutning (Oändlig lutning): Eftersom lutningen $k$ definieras som förändringen i $y$ dividerat med förändringen i $x$, har lodräta linjer en odefinierad eller "oändlig" lutning. Matematiskt uttrycks detta som en division med noll, vilket betyder att vi inte kan tilldela ett tal till lutningen.
Parallellitet: Alla lodräta linjer är parallella med $y$-axeln. Eftersom de inte lutar åt något håll i det horisontella planet, är de alltid parallella med varandra och med $y$-axeln.
Ingen $y$-intercept: Lodräta linjer skär inte $y$-axeln, förutom om de råkar sammanfalla med en axel (vilket bara är fallet när den lodräta linjen är $y$-axeln själv vid $x = 0$).
Grafisk representation
I ett koordinatsystem kan vi lätt rita en lodrät linje genom att:
Bestämma $x$-värdet $a$ där linjen ska vara: T.ex., om $x = 3$, rita en linje parallell med $y$-axeln vid $x = 3$.
Låt $y$-värdena variera: Linjen sträcker sig uppåt och nedåt i oändlighet längs detta $x = a$.
Exempel
Anta att vi ska representera linjen $x = 2$. I ett koordinatsystem ritar vi en lodrät linje som passerar genom alla punkter med $x$-koordinaten $2$, oberoende av vad $y$-koordinaten är:
Några exempel på punkter på linjen är $(2, 0)$, $(2, 1)$, $(2, -3)$, osv.

Lodrät linje: y = 2
Relaterade artiklar
Sannolikhet
Sannolikhet handlar om att mäta hur troligt det är att en händelse kommer att inträffa. Det hjälper oss att förstå och kvantifiera osäkerhet och risk inom olika situationer. Sannolikhet är en central del av statistik och används i många aspekter av vårt dagliga liv. Sannolikhet är användbart inom många områden, inklusive spelteori, statistik, och riskanalys. Det hjälper oss att fatta beslut och förutse resultat i en mängd olika situationer. Enkelt sannolikhetsuppgifter dyker frekvent upp på högskoleprovet så detta är något du måste förstå för att prestera bra på kvantitativa delen.

Mathilde
3 min. läsning
2024-03-16
KVA-delen
KVA-delen på högskoleprovet handlar om "Kvantitativa Jämförelser." Denna del syftar till att testa din förmåga att jämföra och analysera kvantitativa data, såsom siffror, procentandelar och proportioner. Delen är uppbyggd av 20 uppgifter per högskoleprov där den uppskattade tiden är 20 minuter eller 1 minut per fråga. Därför gäller det att snabbt kunna tolka och lösa problemet. Här är en grundläggande förklaring av kvantitativa jämförelser:

Leon
3 min. läsning
2024-03-20
Kvadratuttryck
Kvadratuttryck är användbara inom algebra för att förenkla ekvationer, lösa problem med andragradsekvationer och för att förstå polynomens egenskaper.

Morgan
0 min. läsning
2024-03-16