Avståndsformeln

I ett tvådimensionellt koordinatsystem har vi två axlar:

• x-axeln: Den horisontella linjen

• y-axeln: Den vertikala linjen

De möts vid punkten kallad origo (0,0). Varje punkt i detta system kan identifieras med ett par tal $(x, y)$ som kallas koordinater. Dessa koordinater visar avståndet från origo i horisontell (x) och vertikal (y) ledd.

Anta att du har två punkter i detta system:

• Punkt $A$ med koordinater $(x_1, y_1)$

• Punkt $B$ med koordinater $(x_2, y_2)$

För att hitta avståndet mellan dessa två punkter använder vi avståndsformeln. Enkelt sagt, denna formel är en tillämpning av Pythagoras sats, som används för att beräkna längden på hypotenusan i en rätvinklig triangel.

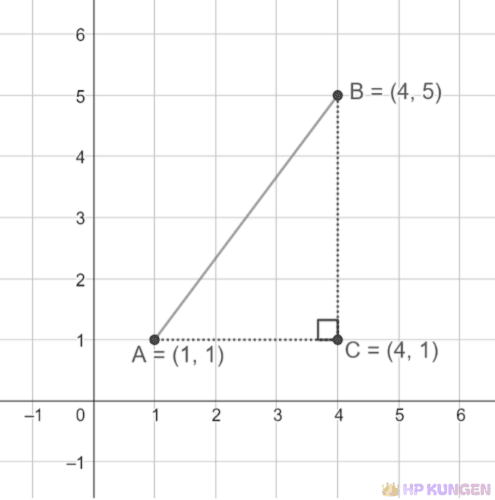
Avståndet mellan två punkter

Avståndet $d$ mellan punkterna $A$ och $B$ kan räknas ut med formeln:

$$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$

Här är en steg-för-steg förklaring för att klargöra detta:

Skillnad i x-led: Beräkna $(x_2 - x_1)$, vilket anger förändringen i x-koordinaterna.

Skillnad i y-led: Beräkna $(y_2 - y_1)$, vilket talar om för oss förändringen i y-koordinaterna.

Kvadrera skillnaderna: Detta innebär att vi multiplicerar skillnaden i x och y med sig själva, alltså $(x_2 - x_1)^2$ och $(y_2 - y_1)^2$.

Addera kvadraterna: Lägg ihop dessa två resultat.

Ta kvadratroten: Slutligen, ta kvadratroten av summan för att få det faktiska avståndet mellan punkterna.