Att bestämma ekvationen för en rät linje

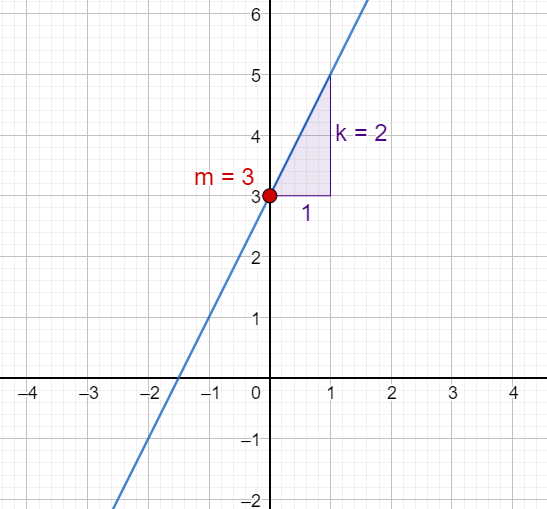
En rät linje kan definieras av en ekvation i form av $y = kx + m$, där $k$ kallas linjens lutning och $m$ är konstanten som kallas $y$-interceptet. Denna ekvationsform kallas k-formen eller k-slope form.

• Lutning ($k$): Lutningen av linjen, $k$, representerar hur brant linjen är. Det beräknas som förändringen i $y$-värde delat med förändringen i $x$-värde mellan två punkter på linjen.

• Y-Skärning ($m$): Detta är punkten där linjen skär $y$-axeln. Det är värdet av $y$ när $x$ är noll.

Rät linje

Ekvationen $y = kx + m$

Låt oss bryta ner ekvationen $y = kx + m$:

$y$: Detta är beroende variabel. Det betyder att dess värde beror på värdet av $x$.

$x$: Detta är den oberoende variabeln.

$k$ (lutning): Om $k$ är positiv, stiger linjen från vänster till höger. Om $k$ är negativ, faller linjen från vänster till höger. Om $k = 0$, är linjen horisontell.

$m$ ($y$-intercept): Det är den punkt där linjen skär $y$-axeln. Om $m$ är större än noll, skär linjen $y$-axeln över origo (ovanför $x$-axeln), om $m$ är mindre än noll, skär den under origo.

Lutningen

Lutningen, $k$, är ett mått på linjens branthet. Om man har två punkter $(x_1, y_1)$ och $(x_2, y_2)$ på linjen, så kan lutningen beräknas som:

$$ k = \frac{y_2 - y_1}{x_2 - x_1} $$

Denna formel återspeglar "ändringen i $y$ dividerad med ändringen i $x$" eller "rise over run."

Bestämma linjens ekvation

För att bestämma en linjes ekvation behöver vi:

Två punkter på linjen: Om vi känner till två punkter, kan vi beräkna lutningen och sedan använda en av punkterna för att lösa för $m$.

En punkt och lutningen: Om vi känner till lutningen och en punkt på linjen, kan vi direkt sätta in dessa värden i ekvationen och lösa för $m$.

Låt oss säga att vi känner till en punkt $(x_1, y_1)$ och vi känner till lutningen $k$, vi kan bestämma $m$ genom att sätta in i ekvationen:

$$ y_1 = kx_1 + m $$

Lös för $m$:

$$ m = y_1 - kx_1 $$

Därifrån kan man skriva ut linjens ekvation $y = kx + m$.

Antag att vi har två punkter $(x_1, y_1)$ och $(x_2, y_2)$. Vi börjar med att beräkna lutningen $k$:

$$ k = \frac{y_2 - y_1}{x_2 - x_1} $$

När vi har lutningen, kan vi använda en av punkterna för att hitta $m$ som i tidigare steg, genom att sätta in i ekvationen:

$$ m = y_1 - kx_1 $$

Nu har vi hela ekvationen för linjen.

Att kunna bestämma ekvationen för en rät linje är inte bara viktigt för matematiska studier, utan det har också tillämpningar i vetenskap, ekonomi och teknik, exempelvis vid modellering av reala situationer med linjär tillväxt eller minskning. För högskoleprovet är förmågan att snabbt känna igen och arbeta med räta linjer i ett koordinatsystem en viktig kompetens.

Denna kunskap möjliggör också en djupare förståelse för mer komplexa koncept inom algebra och analys, såsom linjära ekvationssystem och parametriseringar av funktioner. När man går vidare i matematiken kommer dessa grundläggande insikter att byggas på med ytterligare lager av abstraktion och komplexitet.