Räta linjens ekvation

$$y = kx + m$$

Denna ekvation är en av de mest grundläggande formerna inom algebra och geometri och kan beskriva varje rät linje (som inte är vertikal) i ett koordinatsystem. Låt oss bryta ner varje komponent:

Lutningen, $k$

Lutningen (eller riktningskoefficienten) $k$ anger hur brant linjen är:

• Om $k > 0$, är linjen stigande.

• Om $k < 0$, är linjen fallande.

• Om $k = 0$, är linjen horisontell.

Lutningen räknas ut genom förändringen i $y$ dividerat med förändringen i $x$ mellan två punkter $(x_1, y_1)$ och $(x_2, y_2)$ på linjen:

$$ k = \frac{y_2 - y_1}{x_2 - x_1} $$

Denna konstans ger en känsla av linjens typ och är central för att skriva eller manipulera linjens ekvation.

Y-Skäringspunkt, $m$

Y-interceptet $m$ är den punkt där linjen skär y-axeln, det vill säga då $x = 0$. Det är värdet på $y$ när linjen korsar y-axeln och indikerar linjens position i förhållande till origo.

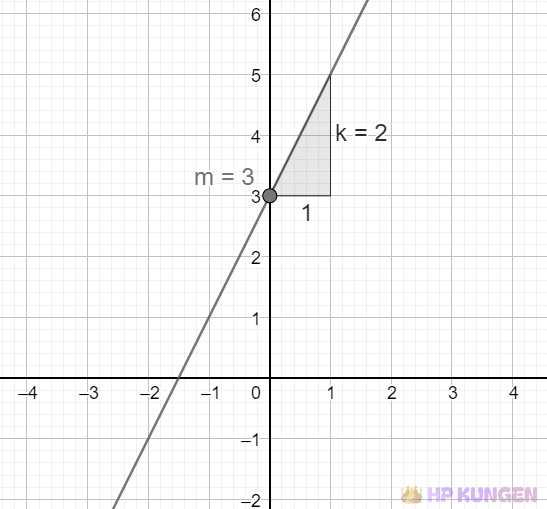
Rät linje

För att tillämpa räta linjens ekvation:

Ge en bestämd punkt och lutning: Om vi vet att en linje har en lutning $k = 2$ och går genom punkten $(1, 3)$, substituerar vi i punkt-korsprungsform för att hitta $y$:

$$ y - 3 = 2(x - 1) $$

Expressionen behöver manipuleras för att passa $y = kx + m$, vilket ofta är formatet vi önskar.

Beräkna lutningen mellan två punkter: Om linjen går genom punkterna $(2, 4)$ och $(4, 8)$, är lutningen $k = \frac{8-4}{4-2} = 2$.

Exempel:

Nedan är ett exempel på den räta linjen $y=2x-2$

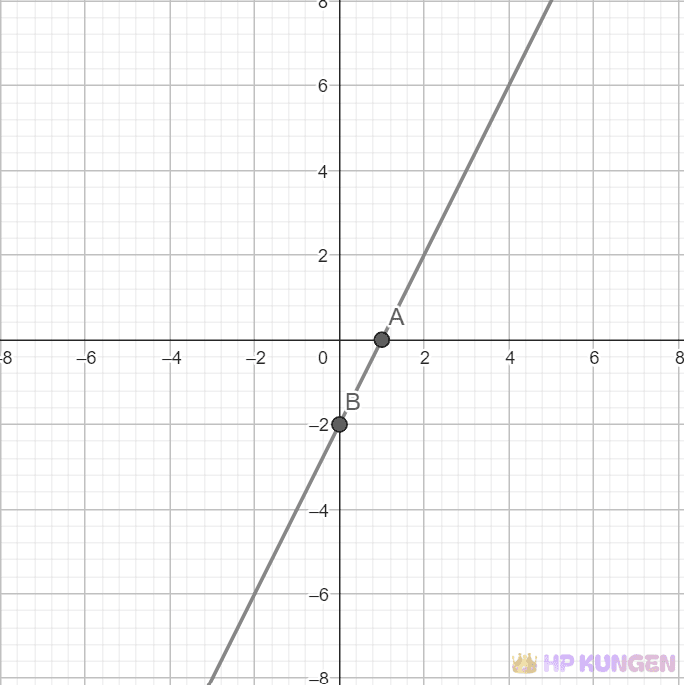
y=2x-2

Att förstå och kunna arbeta med räta linjens ekvation är en grundläggande färdighet inom matematik. Den hjälper till att lösa geometriska problem, förstå grafer och deras betydelse — färdigheter som är väsentliga inför bland annat högskoleprovet.

Det är viktigt att kunna både konceptuellt beskriva vad ekvationen innebär och använda den praktiskt, inklusive att kunna övergå mellan olika representativa former vid behov. Det bygger en grund för mer avancerade matematiska kurser och problemställningar.