Koordinatsystem introduktion

I grund och botten är ett koordinatsystem ett sätt att ange positioner på en yta. Det vanligaste koordinatsystemet i gymnasiematematik är det tvådimensionella kartesiska koordinatsystemet. Detta system består av två vinkelräta linjer: en horisontell x-axel och en vertikal y-axel, som möts i en punkt kallad origo (0,0).

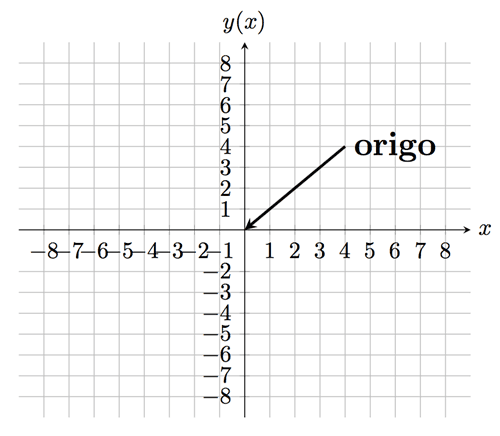
Koordinatsystem

Varje punkt i detta plan kan representeras med ett par av tal, kallas koordinater, skrivna som $(x, y)$. Här representerar $x$ punkten horisontella avstånd från origo, och $y$ representerar vertikala avstånd från origo. Till exempel, om vi har en punkt med koordinater (3, 2), betyder det att punkten ligger 3 enheter åt höger och 2 enheter upp från origo.

Koordinatsystemet är uppdelat i fyra kvadranter baserat på tecknen på x- och y-koordinaterna:

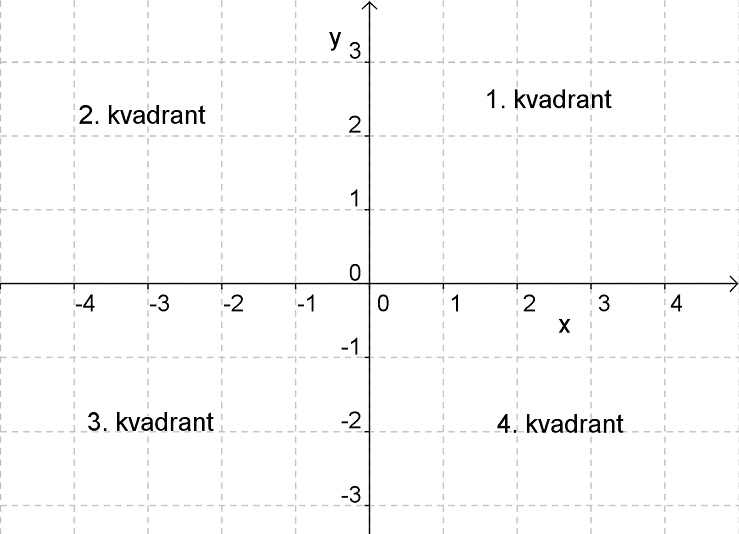
Kvadranter koordinatsystem

Första kvadranten: $x > 0$ och $y > 0$

Andra kvadranten: $x < 0$ och $y > 0$

Tredje kvadranten: $x < 0$ och $y < 0$

Fjärde kvadranten: $x > 0$ och $y < 0$ Dessa kvadranter hjälper till att snabbare kunna lokalisera och förstå positionen av en viss punkt i förhållande till origo.

I ett kartesiskt koordinatsystem kan vi använda ekvationer för att rita grafer och därigenom visualisera relationer mellan olika variabler. En av de enklaste formerna av en ekvation i ett koordinatsystem är den för en rak linje.

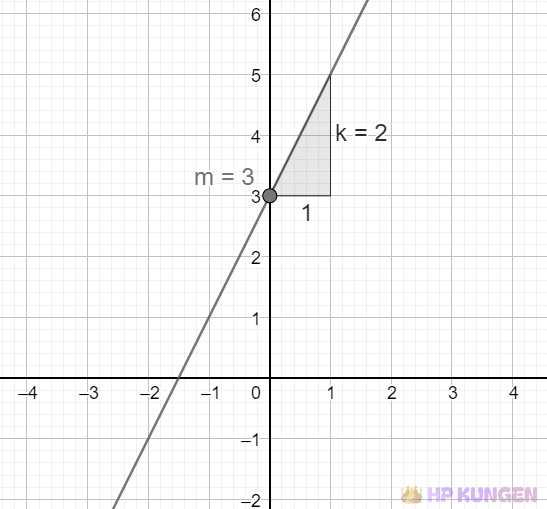
Linjens ekvation

Den allmänna formen av en linjens ekvation i ett plan är $$ y = kx + m $$ där: $k$ är linjens lutning (hur mycket y-värdet ändras för varje enhetsändring i x), $m$ är y-värdets skärningspunkt (den punkt där linjen skär y-axeln). Om $m = 2$, betyder det att för varje enhet vi rör oss i x-led, ökar y-värdet med 2 enheter. Detta är viktigt när vi analyserar trender och relationer i data.

Lutning och skärning

Lutningen $m$ anger hur brant linjen är. Om $k > 0$, är linjen stigande, om $k < 0$, är den fallande, och om $k = 0$, är linjen horisontell. Skärningspunkten $m$ visar oss var linjen korsar y-axeln, en bra referens för att rita linjer.

Rät linje