Funktioner
Utforska området tillsammans med HP Kungen.
En funktion i matematiken är som en maskin som tar ett nummer som inmatning och ger oss ett annat nummer som utmatning. Du kan tänka på det som en regel som beskriver hur ett nummer förändras till ett annat. En funktion representeras oftast som $f(x)$ eller $y$, där $x$ är ingången (ingångsvärdet) och $f(x)$ eller $y$ är utgången (resultatet).
Förstagradsfunktioner
En förstagradsfunktion är en typ av funktion som representerar en rät linje. Denna typ av funktion har formen:
$$y = kx + m$$
Där $k$ är lutningen (stigningen) på linjen och $m$ är skärningspunkten med y-axeln (värdet av $y$ när $x = 0$).
Lutning (k)
Lutningen, $k$, mäter hur brant linjen är. Den beskriver hur mycket $y$-värdet ökar eller minskar när $x$ ökar med en enhet. Lutningen kan beräknas med följande formel:
$$k = \frac{y_2 - y_1}{x_2 - x_1}$$
Där $(x_1, y_1)$ och $(x_2, y_2)$ är två punkter på linjen. Lutningen är kvoten av förändringen i $y$ till förändringen i $x$ mellan dessa två punkter.
Vinkelräta Linjer
Två linjer sägs vara vinkelräta mot varandra om produkten av deras lutningar är -1. Detta innebär att om $k_1$ och $k_2$ är lutningarna för två linjer, så gäller följande villkor för vinkelräta linjer:
$$k_1 \cdot k_2 = -1$$
Detta är användbart när du vill bestämma om två linjer är vinkelräta mot varandra.
Låt oss säga att vi har en linjär funktion $y = 2x + 3$. Här är $k = 2$ (stigningen) och $m = 3$ (skärningspunkten med y-axeln). Om vi vill hitta lutningen mellan två punkter, säg $(1, 5)$ och $(3, 9)$, kan vi använda formeln:
$$k = \frac{9 - 5}{3 - 1} = \frac{4}{2} = 2$$
Så, lutningen är 2, vilket innebär att linjen är rät och går uppåt.
Detta är en grundläggande översikt över förstagradsfunktioner och de viktiga begreppen som hör ihop med dem. Linjära funktioner är grundläggande inom matematiken och används i många praktiska tillämpningar.
Grafen till funktionen $f$ är en rät linje genom origo. $a> 0$
Kvantitet 1
$ f(a)$
Kvantitet 2
$ f(-a)$
Andragradsfunktioner
Andragradsfunktioner är en annan typ av funktion där grafen inte är en rak linje, utan en parabel. De har formen:
$$f(x) = ax^2 + bx + c$$
Där $a$, $b$, och $c$ är konstanter. $a$ påverkar öppningen och riktningen på parabeln, $b$ påverkar dess position längs x-axeln, och $c$ påverkar dess position längs y-axeln.
Exempel: Låt oss säga att vi har en andragradsfunktion $f(x) = x^2 - 4x + 4$. Vi kan använda den för att beräkna värden som $f(2) = 2^2 - 4 \cdot 2 + 4 = 0$. Så när $x = 2$ är $f(x) = 0$.
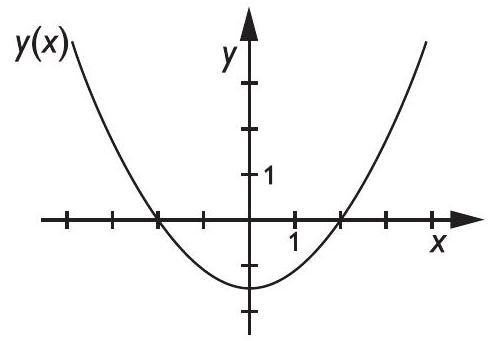
$y(x)=a x^{2}-\frac{3}{2}$ Vad är konstanten $a$?
1. Funktioner tar in ett värde och ger oss ett annat.
2. Linjära funktioner är raka linjer och har formen $f(x) = kx + m$.
3. Andragradsfunktioner är parabler och har formen $f(x) = ax^2 + bx + c$.
För att använda funktioner behöver du bara sätta in ett värde för $x$ och räkna ut $f(x)$. Detta är grunden för att förstå många matematiska koncept och tillämpningar.
Öva på Funktioner
Öva på Funktioner genom att lösa uppgifter som kommer på högskoleprovet.