Parallella linjer
Daniel
Civilingenjör i datateknik - KTH
1 min. läsning
för 2 år sedan
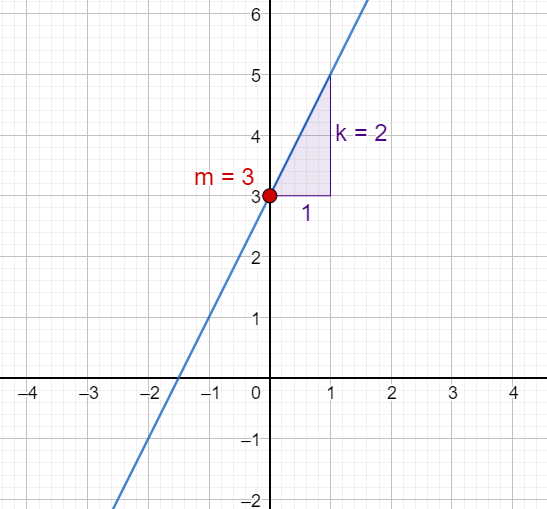
Parallella linjer är linjer som aldrig skär varandra, oavsett hur långt de förlängs i båda riktningar. I ett koordinatsystem innebär detta att de har samma lutning men olika $y$-intercept, vilket betyder att de alltid är lika avstånd från varandra.
Egenskaper hos parallella linjer
Samma lutning ($k$): De har samma lutning, vilket är den avgörande egenskapen för parallellitet. Om två linjer har ekvationerna $y = kx + m_1$ och $y = kx + m_2$, där $k$ är detsamma i båda ekvationerna men $m_1 \neq m_2$, är dessa linjer parallella.
Aldrig skärning: Eftersom de har samma lutning men olika $y$-intercept, kommer de aldrig att mötas. De är som två spår på en järnväg.
Matematisk beskrivning
Om vi har två linjer med ekvationerna:
Linje 1: $y = kx + m_1$
Linje 2: $y = kx + m_2$
Där lutningen $k$ är densamma men intercepten $m_1$ och $m_2$ är olika, är dessa linjer parallella. Detta är en direkt följd av att lutningen avgör linjens riktning i planet.
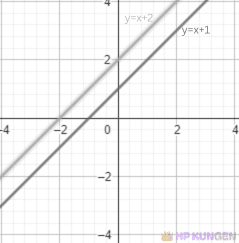
Parallella linjer
Grafisk representation
För att visualisera parallella linjer i ett koordinatsystem gör man så här:
Rita den första linjen: För given lutning $k$ och $y$-intercept $m_1$, rita den första linjen.
Rita den andra linjen: För samma lutning $k$ men annat $y$-intercept $m_2$, rita den andra linjen.
Notera lutningen: Båda linjerna kommer att ha samma lutning, vilket innebär att de har samma vinkel mot $x$-axeln och aldrig kommer att mötas.
Exempel
Låt oss säga att vi har två linjer med ekvationerna:
Linje 1: $y = 2x + 3$
Linje 2: $y = 2x - 4$
Båda dessa linjer har lutningen $k = 2$, vilket betyder att de är parallella.
Relaterade artiklar
Potenser
Dessa potensregler är användbara verktyg inom matematik och används för att förenkla och utforska uttryck med potenser och exponenter. De tillämpas i olika matematiska områden och är grundläggande för att lösa problem som involverar potenser och exponenter. Detta är väldigt viktigt att veta inför högskoleprovet då det ofta förekommer uppgifter som inkluderar följande regler.
Leon
1 min. läsning
2024-03-16
Bråk
Ett bråk är en matematisk representation av en del av en helhet. Det är ett sätt att dela upp något i mindre delar. Bråk består av två delar: en täljare och en nämnare. Täljaren representerar antalet delar du har, medan nämnaren representerar det totala antalet delar i helheten. Bråk är användbara för att representera delar av en helhet, och de används i en mängd olika situationer inom matematiken och vardagen. Det är viktigt att förstå de grundläggande reglerna för bråk eftersom de är grunden för många andra matematiska koncept och dyker frekvent upp på högskoleprovet.
Morgan
1 min. läsning
2024-03-16
Vetenskapliga termer
Högskoleprovet omfattar ofta uppgifter och texter som rör sig inom naturvetenskap, samhällsvetenskap eller teknik, där användningen av specialiserad terminologi är oundviklig. Att behärska dessa termer är inte bara en nyckel till att tolka och svara på frågor korrekt, utan det underlättar även förståelsen av komplexa texter och uppgifter vilket ger dig en fördel på högskoleprovet! Här i listan nedan är några vanliga prefix och suffix för vetenskapliga termer.
Nora
1 min. läsning
2024-03-16